Five fold – Cobalt tricyanomethanide
What is it?

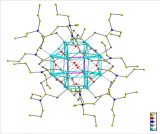
The beautiful shapes of crystals are not a fluke – they reflect the symmetries of the atoms within the crystal. Those atoms (and molecules), however, can only have certain types of symmetries. Five-fold symmetry, for example, is not possible (except for quasicrystals, which are a whole different story…). You can prove this to yourself – try covering the whole surface of a table only with regular pentagons. Can't do it, can you? There are always those annoying gaps. So when the beautiful pentagonal "crystals" shown above were discovered in a reaction, there had to be more going on. For a crystallographer five fold symmetry sets off alarm bells.
It turns out that these crystals weren't individual crystals at all, but rather collections of five individual wedge-shaped crystals growing together to form a pentagon. The structure of the crystals was solved by carefully cutting out one of these wedges and performing X-ray diffraction on this. If the pentagon had been used instead it would have been a horrible, unsolvable mess, with five diffraction patterns superimposed on each other, all in different orientations.
Solving the crystal structure revealed not only the molecular structure of the crystals, but also solved another curious observation. While the compound made with cobalt formed the lovely orange pentagons you see here, similar compounds with other metals formed pentagons with wedges missing. Even more unusually, crystals of the copper analogue didn't form the pentagons at all.
The key to solving this riddle was the fact that the lovely sharp arrangement of faces on a crystal is related to the arrangements of simple planes of atoms within the crystal (as I said before, the shapes of crystals are related to the symmetry of the atoms within). In the structures in question, there are two very simple planes in the crystals that are angled at approximately 72°, which is exactly the right angle you need for the corner of the wedges that come together in the middle of the pentagon. For the cobalt structure, that angle was 71.2°, and only pentagons formed. For the other structures, results and angles varied. Mn (71.7°) and Cd (72.2°) were closer to the magic 72°, but maybe too close for comfort. These only formed pentagons with wedges missing, or wedges by themselves. Zn, with an angle further away (70.9°), was similar. Ni (70.8°) formed pentagons, but they were very small and too a lot of effort to make. Cu, with the greatest deviation from 72° (67.3°), formed no pentagons at all.
What does it look like?
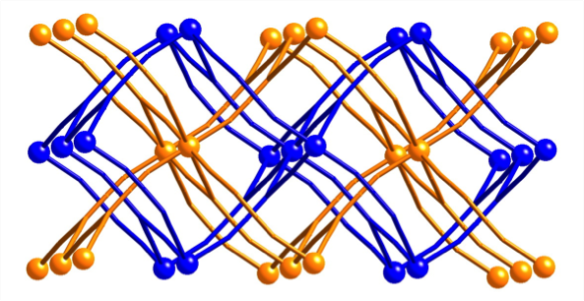
So after all that, what was the structure? It turned out that the structure was very closely related to that of the mineral rutile. In these new structures, however, the titanium atoms in rutile were replaced by the transition metals listed above, and the oxygen atoms were replaced by the larger tricyanomethanide anion. Because the anion was much larger in new structures, there was room enough in the structure for not one but two networks to coexist, weaving through each other (but never touching) in an intricate dance known as interpenetration. It pays to look at your crystals closely. Their shape can tell you something if you're taking notice.
Where did the structure come from?
"Crystal structures and magnetic properties of the interpenetrating rutile-related compounds M(tcm)2 [M = octahedral, divalent metal; tcm- = tricyanomethanide, C(CN)3-] and the sheet structures of [M(tcm)2(EtOH)2] (M = Co or Ni)", S. R. Batten, B. F. Hoskins, B. Moubaraki, K. S. Murray and R. Robson, J. Chem. Soc., Dalton Trans., 1999, 2977.
CCDC Refcode: LORGAA